Introduction

Im ważny kierunek drgań w diagnostyce silników turbinowych lotnictwo i maszyn wirnikowych jest diagnostics poprzez modelowanie. Modelowanie daje możliwość powiązania obecnośćniektórych rodzajów wad maszyn z oznak jego obecności w sygnale drgań. Jednym z takich wad jest pojawienie się pęknięć w wałach silników lotniczych i maszyn przepływowych, co jestniedopuszczalne. Więcnajważniejszym zadaniem systemu diagnostycznego jest wykrycie pęknięcia w czasie i prognozy jej rozwoju.

Appearance pęknięcia w wyniku wirnika miejscowego spadku sztywności. Wartość utraty sztywności zależy od cech geometrycznych pęknięcia. Jeśli obciążenie statyczne, takie jak siła ciężkości jest wywierana, pęknięcie otwiera się i zamyka się, gdy wirnik się obraca. W rezultacie, sztywność wału zmienia się za pomocą cyklu. Pęknięć w przewodach układu wirnika\ following zmiany drgań sygnału [1]:

increase amplitudy 1x harmonicznej od prędkości obrotowej dzięki wzrostowi odchylenia statycznego spowodowane zmniejszeniem sztywności.

appearance 2x składowej prędkości obrotowej wirnika, ze względuna asymetryczny sztywności.

appearance z 3х składowej prędkości obrotowej, w wyniku cyklicznego otwierania i zamykania szczeliny.

101; pęknięcie odbywa się pod uwagę, jak wiele czynników, jak to możliwe.&#\Liczba różne podejścia, aby symulować pęknięcia. Wnajprostszych przypadków pęknięć symulowane przez zmniejszenie promieniowej sztywności całego wału [2,3,4]. W innych przypadkach, to część wału, wywoływanie

101; pęknięcie ma miejsce, jest replac&101 d równoważnym elementem belki. Współczynniki macierzy sztywności tego elementu są obliczane biorąc pod uwagę pęknięcia i zmianyna cykl. W pracy [5] Obliczenie sztywności matrycy elementu belki z pękać ze względuna zastosowanie momentów bezwładności przekroju belki rozważa pęknięcie. W pracy [6] macierzy sztywności takiego elementu jest obliczanana podstawie równań mechaniki zniszczenia ciał stałych. Pęknięcie może być symulowane przez elastyczne łącza odcinków brzegowych łączenia wału w miejscu jego lokalizacji inadając tej chwili pęknięcie sztywność [7,8].#&\#Zmień pęknięć sztywności w zależności od jego otwierania i zamykania, gdy wirnik się obraca może być opisana matematycznie w różny sposób. Wnajprostszym przypadku można przyjąć, że szczelina ma tylko dwa położenia: całkowicie

\opened lub całkowicie zamknięte, a funkcja etap może być stosowany w celu opisania jego zmiany sztywności matematycznie [4]\. Work [3] opisujenajbardziej rozpowszechnionym modele zmiany sztywności. Jednym znich jest równanie Gasch. Zmiana\w sztywności odbywa się w zależności od kąta między fazą siły statyczne i fazie pęknięcia i opisanych przez 17 harmonicznych szeregu Fouriera. W tym samym artykule podaje Maes

101; sztywność zmienia się w zależności od kąta, zgodnie z prawem cosinus. W modelu Yang sztywność zmian przez prawie cosinus w stopniu względnej głębokości pęknięć.

W artykuł rozwija model pęknięćna podstawie&&#

\ID algorytm jest włączony do programu Dynamics R4 [9], co stanowi dedykowany \systemna obliczenie dynamicznej złożonych systemów wirnika.

Crack

Within Zaakceptowana koncepcja symulacji, pęknięcia w modelu wału otrzymuje elastycznego łącza dzielącym wałuna dwie części i opisującym sztywnością matrycy o zmiennej współczynników. Jeślinie ma pęknięć, stan szczep kompatybilność pomiędzy sekcjami części wału jest realizowane, więc wszystkie wzajemne przemieszczenia są zabronione. Wprowadzamy obrotowy układ współrzędnych ηOε leży w obszarze pęknięcia, figura 1. Jego pokrywa pochodzenia z początkiemnieruchomej systemu współrzędnych XYZ. Wał wykonuje dwa ruchy - właściwy ruch obrotowy i precesji wokół osi Z. Opisując pęknięcia weźmiemy pod uwagę jedynie obrót wokół osi rj i ε. Przesunięcia w innych stopniach swobody są pomijane.

 \\ sekcjaFigure 1. Pęknięcie

Flexibility matrycy odnośnik symulowania pęknięcie obracającego się układu współrzędnych może być zapisana jako \ following  

  \ \wher

\Q

jd

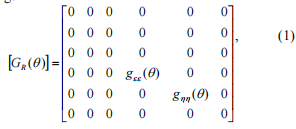
 j &#\\ wał kąt obrotu \d \\ kąt precesji;=-g ee-\\ ( q )-g HH\ (Q- \\)zmienny\coefficients od momentu elastyczności \\.\ Flexibility zależy od kąta QWyniki gdy wał obraca się, pęknięcie otwiera się i zamyka. Sztywność matrycę otrzymuje się przez inwersję\\ [ GR-\\ ( q\\)\\]matrix i zerowych współczynników elastyczności w głównej przekątnej prowadzić do uzyskiwania współczynników sztywności idzie donieskończoności. Ograniczyć wartości współczynników sztywności przez 1е10 Nm; Założenie tonie wpływa znaczącona wynik, to otrzymujemy\

   Stiffness matrycy przekształca się stały układ współrzędnych za pomocąnastępujące równanie:\\ wywoływanie101;\\ [T\\]/\\ macierz obrotu (4), wywoływanie

101;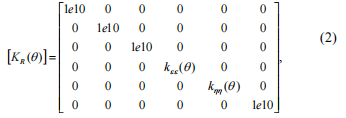C

 \\ \\ podoficerów (  j) s

1\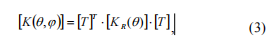

j \\) &#\\ Pomnożenie matryce odpowiednio do równania (3) otrzymujemy:.-&#\=przeprowadzenia pewnych przekształceń, które dają możliwość przejścia do uproszczenia opisu szczelinystiffness matrycy i jej algorytmu uzyskiwania współczynników. Odpowiednio do modelu Maes, to\may przyjąć, że promieniowy elastyczność okrągłego belki ze zmianami pęknięć od minimalnej do maksymalnej wartości przez prawo cosinus.=\\ wywoływanie

101;

0 elastyczność belki bez pęknięć (minimalną wartość) gc

\\ elastyczność belki z otwartymi\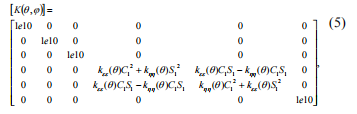crack (wartość maksymalną).

 Zostana wymienić pęknięcia zawiasem z chwili sztywności  \k init \

H

\\. Wiązka warunki brzegowe powinno dostarczyć

statical definiowalności, jak to pokazanona rysunku 2.\  &#-Figure 2 . Zastąpienie pęknięciana zawiasie\- 

Then promieniową elastyczność pasemek przekrój wału z otwartą szczelinę w postaci:   \\ wher 101;E\\ moduł YoungaI  \\ średnicowy momentem bezwładności części wału\k init \

\   

\\